Prediction of human skin permeability using artificial neural network (ANN) modeling¹

Introduction

Skin permeability is of relevance to a number of applications including the design of skin cream products, risk assessment of hazardous chemicals, and in particular, transdermal delivery of drugs. There has been a continuous interest in predicting skin permeability since Scheuplein^[1,2] and Scheuplein and Blank^[3,4] first introduced anatomically-based physicochemical models describing percutaneous absorption. This is partly due to ethical difficulties with respect to human and animal experiments and partly due to economic considerations and increasing legislation in the risk assessment of industrial chemicals, for example, the newly-proposed European chemicals strategy: Registration, Evaluation, Authorization and Restriction of Chemicals (REACH)^[5].

Previous studies on predicting skin permeability can be categorized into mechanistic and empirical models^[3,6,7]. The advantage of many mechanistic models is that they can provide insights into the mechanisms of skin permeation. However, most mechanistic models are complex in nature and several challenges remain for practical use. A main challenge is that mechanistic models involve parameters that are not easily measurable and attainable. Assumptions also have to be made. Some assumptions may be oversimplified and not necessary apply to real situation. In the domain of skin permeability prediction, empirical models have been also frequently reported^[8]. Many empirical models employ the so-called quantitative structure-activity relationship (QSAR) methods which attempt to relate statistically the biological activity of a series of compounds to their physicochemical and/or structural properties^[9]. QSAR methods, stretching back over a century, had been applied in many fields^[10,11]. In the last 30 years, QSAR methods had been developed to relate percutaneous penetration properties of a range of chemical compounds to their physicochemical parameters. Compared with the mechanism model, the QSAR model for skin permeability does not consider the dynamic process of skin permeation. Most QSAR models for skin permeability work well within the range of the experimental data, but often can not be extrapolated. From the point of view of practical application, the approach is simple and can provide acceptable predictions once validated. Various QSAR models for skin permeability have been reported. Moss et al^[8] recently gave a comprehensive review on different QSAR models for skin permeability. An early study by Potts and Guy^[12] analyzed the data of Flynn^[13] and related the skin permeability of the analyzed compounds to their octanol-water partition property and molecular weight. They proposed the empirical equation of skin permeability as log K_p=0.71log K_ow -0.0061MW-6.3, where log K_p is skin permeability is given in cm/s, log K_ow is solute partition coefficient in octanol/water, MW is molecular weight. Different empirical equations were also proposed by other researchers using other structural molecular parameters such as the number of hydrogen bonds and molecular volume^[14,15]. Most QSAR models for skin permeability employed the multiple linear regression (MLR) method. The method provides an efficient way to determine the most relevant physicochemical descriptors. The main drawback of the MLR approach is that it assumes linearity between the descriptors and skin permeability. The artificial neural network (ANN) is similar to the MLR approach, but is more suitable for extracting both linear and nonlinear effects of chosen descriptors on skin permeability. Recently, Degim and colleagues^[16,17] used the ANN model to predict skin permeability. The dataset was limited to 40 chemical compounds in the range of -0.77≤logK_ow≤4.57 and 32 Da≤MW≤ 389 Da. The descriptors used include the partial charge, log K_ow and MW of each compound. Abraham et al^[18] argued that log K_ow was an empirical colligation variable and did not give the actual structural features of the chemical compounds that influence skin permeability. Therefore, some researchers have related skin permeability to Abraham descriptors which they believe can better describe the actual features of molecules and improve the precision of the model^[19].

In this paper, we report that the ANN model predicts skin permeability of chemicals using Abraham descriptors. A large database of skin permeability containing 215 data points was compiled from literature. The correlation between the skin permeability coefficient and the Abraham descriptors were obtained from the trained neural network. In addition, the predictability of the neural network model was compared to the MLR model. The ANN model was shown to give better prediction results which indicate non-linearity and complexity of correlation between Abraham descriptors and skin permeability. Some insight into the degree of nonlinear behavior of every Abraham descriptors has also been assessed with a functional dependence to understand relationships.

Materials and methods

Data set A structurally-diverse set of compounds was selected to construct the MLR and ANN models (n=215, -2.11≤log K_ow≤7.6, 18 Da≤MW≤518 Da, -0.85≤log K_p (cm/h)≤ -5.22). Skin permeability data expressed in log K_p (cm/h), were obtained from literature and regulatory sources^[13,20,21]. Abraham descriptors of R₂ (excess molar refraction), π₂^H (the dipolarity/polarizability), Σα₂^H, Σβ₂^H (the overall or effective hydrogen-bond acidity and basicity), and V_x (the McGowan characteristic volume) were obtained using Abraham Solvation Parameters (ABSOLV) program (Pharma Algorithms Software, Toronto, Canada). The program was written to read molecular structures as Simplified Molecular Input Line Entry System (SMILES) strings which were obtained from the PubChem net database^[22]. The dataset is listed in Table 1.

Table 1 Names, R₂, π₂^H, Σα₂^H, Σβ₂^H, and V_x of the compounds used in the study.
Full table

Prediction models The chemical compounds were listed alphabetically according to their chemical names and divided into 5 subsets. Details about the division of the sub-datasets are also shown in Table 1. Subsets 1, 3, and 5 were used as the training dataset, subset 4 as the validation dataset, and subset 2 as the testing dataset. For comparison, a MLR model had also been generated using subsets 1, 3, 4, and 5. The Neural Network Toolbox of MATLAB 7.0.2 was used to construct the ANN model. Back-propagation networks had been employed in this study. There are some empirical rules about constructing artificial neural networks, for example, 2 hidden layers are sufficient for generality^[23]. The number of units of the hidden layer normally is not more than twice the input ^[24]. In our example, there were 5 inputs corresponding to the 5 Abraham descriptors and 1 output for skin permeability. To determine the ANN architecture, all network structures with the maximum allowed numbers of hidden layers and hidden units limited to 2 and 10, respectively, had been investigated. Each network was trained by 3-folding cross validation using the 3 subsets 1, 3, and 5. For the training of each network, the average mean square errors (MSE) between the model prediction and experimental data were obtained. The ANN architecture with the smallest average value of MSE was chosen. The MSE is defined as follows:

(1)

where log K_p,obs is the experimental value, log K_p,cal is the predicted value, and N is the number of data points in the training dataset.

After determining the ANN architecture, the 3 subsets of 1, 3, and 5 were combined with subset 4 to further tune the ANN parameters to obtain the final ANN model. Finally, subset 2 that had not been used for training the network was used to test the predictability of the model. The same subset 2 was also used to test the MLR model. The early-stopping method was used for the training and validation.

Results

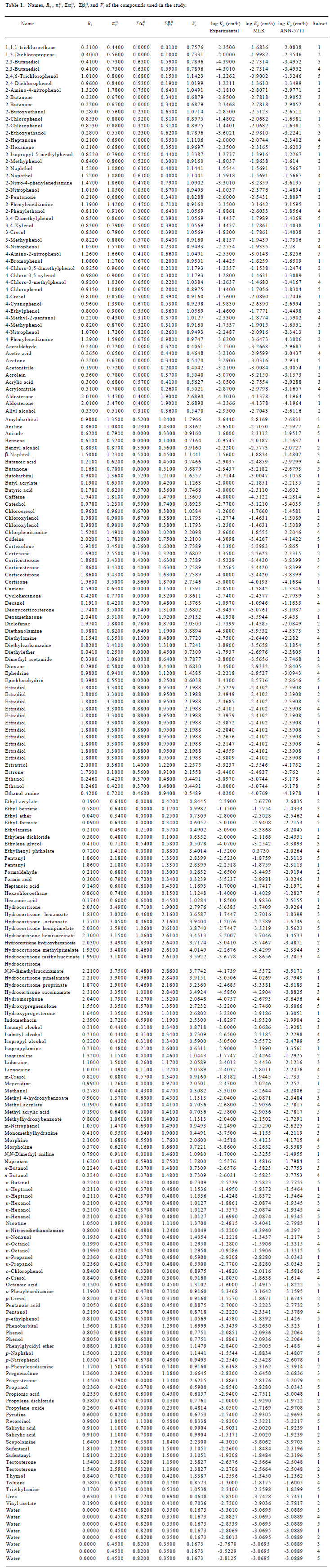
Comparison between the MLR and ANN models The best ANN structure with minimal MSE contained 7 neurons at the first hidden layer and 1 neuron at the second hidden layer. The model was described as ANN-5711, which corresponded to a minimal MSE of 0.10511. Figure 1 shows the relationship between predicted values and experimental results. The statistical test results for the ANN model are shown in Table 2.

Figure 1 Comparison of experimental data with predictions made with ANN model. Line represents 1 to 1 correspondence line.

Table 2 The statistical test results of ANN model.
Full table

Many previous QSAR models for skin permeability were based on the MLR method. Here, for comparison, subsets 1, 3, 4, and 5 were also used to build a MLR model using the 5 Abraham descriptors. The best-fitted equation was as follows:

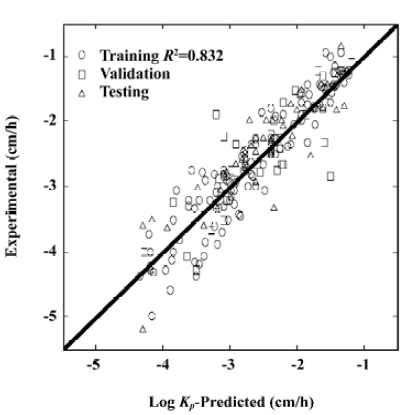
When using the above equation, the MSE for the predicted log K_P was found to be 0.25 for datasets 1, 3, 4, and 5, and 0.21 for the testing dataset 2. Figure 2 shows the relationship between the experimental results and predicted values using the MLR model of equation 2. The statistical test results for the MLR model are shown in Table 3.

Figure 2 Comparison of experimental data with predictions made with MLR model. Line represents 1 to 1 correspondence line.

Table 3 The statistical test results of MLR model.
Full table

For the training dataset, the R² and MSE of the MLR model was 0.70 and 0.25, respectively. However, the ANN model on the same training dataset produced much improved results with R²=0.841 and MSE=0.133, respectively. For the testing dataset, the ANN model improved the R² of the MLR model by 12% and the MSE value by 30%. For the whole dataset, the MLR model produced a R² value of 0.699. This coefficient was improved to 0.832 with the ANN model. The MSE value of the MLR model was 0.243 which compares with a much-reduced value of 0.136 for the ANN model. Clearly, the ANN model can better predict skin permeability from Abraham descriptors (Table 4).

Table 4 Comparison between MLR and ANN models.
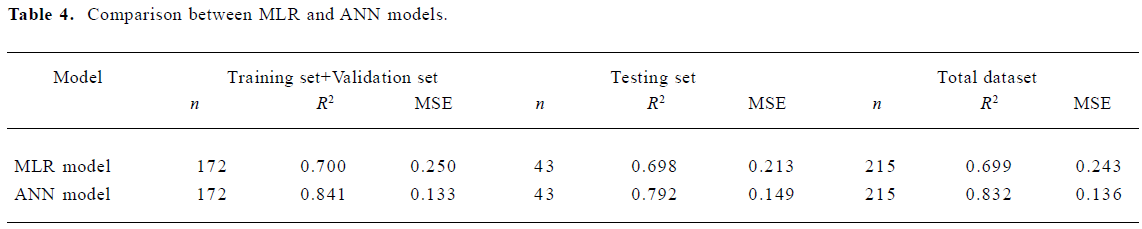
Full table

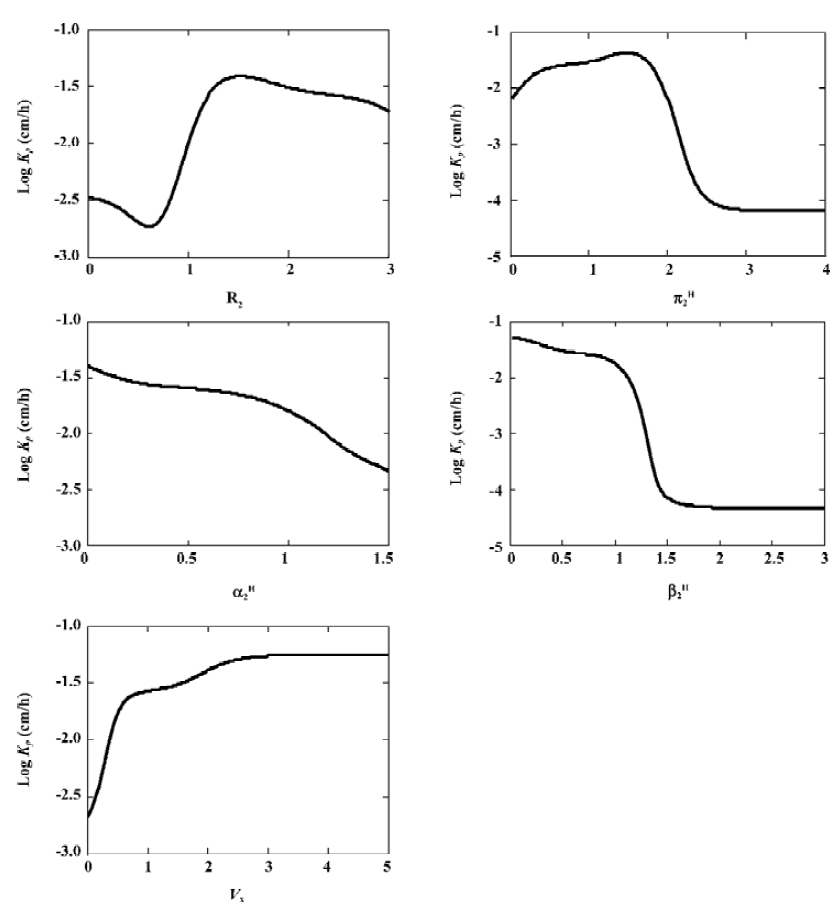
Dependence of skin permeability on the descriptors The ANN model was used to analyze the influence of each Abraham descriptor. Skin permeability was calculated using the ANN model by varying 1 Abraham descriptor each time while keeping the rest of the descriptors constant mean value of each range. The results are shown in Figure 3.

Figure 3 Dependency of permeability log K_p on the single descriptor for ANN model. The descriptors not shown in the plots were set to their median values.

Discussion

Generally, log K_p has inversely depended on π₂^H, the solute polarity. The statum corneum (SC) lipid phase is mainly composed of hydrocarbon substance. It is well known that solute partition into the lipid phase decreases in the hydrocarbon solvents with increasing solute polarity. The relationship between skin permeability and the partition coefficient can be expressed by the following equation:

where K_m is the skin-water partition coefficient of the solute, D is its diffusivity through the skin, and δ is the diffusion path length.

Σα₂^H and Σβ₂^H reflect solute hydrogen bonding activity. Many researchers have discussed the relationship between hydrogen bonding and skin permeability^[15,19], and have suggested an inverse relationship between them. This was also observed in this study. The reason is similar as that of π₂^H; the increasing solute hydrogen bond acceptor and donor activity resulted in decreased partitioning into the organic phase due to the free energy cost associated with the disruption of hydrogen bonds^[19]. It is interesting to note that in the MLR model there was a positive relationship between Σα₂^H and log K_p. This suggests that although the MLR model has reasonable precision, it may not be necessary to provide correct relationships between skin permeability and some of the Abraham descriptors.

Predicted skin permeability increased with the McGowan characteristic volume descriptor. This was not expected. A similar, unexpected relationship was observed before by Potts and Guy^[19]. They explained that the molecular volume represented a combination of physical phenomena: the impact of molecular size on partition and diffusion. On the one hand, increasing molecular size increased the hydrophobic surface area and this increased the partitioning into a lipid phase. On the other hand, larger molecules diffused more slowly, leading to reduced permeability. The positive relationship between K_p and V_x tends to suggest that partitioning effects dominate.

The effect of R₂ on skin permeability is rather complex. In previous studies, Potts and Guy have suggested that the effect of R₂ was not significant ^[19].

An artificial neural network model for predicting skin permeability was developed and compared with a multiple linear regression model. The model was based on a comprehensive set of experimental data from various sources in the open literature. Both the MLR and ANN (ANN-5711) models are related to Abraham descriptors. Compared to the MLR model, the ANN model was shown to give better prediction results which indicate non-linearity and complexity of correlation between Abraham descriptors and skin permeability. Some insight into the degree of nonlinear behavior of every Abraham descriptors has also been assessed with a functional dependence to understand relationships.

References

1. Scheuplein RJ. Mechanism of percutaneous adsorption. I. Routes of penetration and the influence of solubility. J Invest Dermatol 1965;45:334-46.
2. Scheuplein RJ. Mechanism of percutaneous absorption. II. Transient diffusion and the relative importance of various routes of skin penetration. J Invest Dermatol 1967;48:79-88.
3. Scheuplein RJ, Blank IH. Permeability of the skin. Physiol Rev 1971;51:702-47.
4. Scheuplein RJ, Blank IH. Mechanism of percutaneous absorption. IV. penetration of nonelectrolytes (alcohols) from aqueous solutions and from pure liquids. J Invest Dermatol 1973;60:286-326.
5. CEFIC. CEFIC Workshop on methods to determine dermal permeation for human risk assessment. Utrecht: Institute of Occupational Medicine; 13–15 June 2004. Report No.: TM/04/07.
6. Guy RH, Hadgraft J. A theoretical description relating skin penetration to the thickness of the applied medicament. Int J Pharm 1980;6:321-32.
7. Wang TF. Microscopic models for the structure and permeability of the stratum corneum barrier layer of skin [PhD thesis], Buffalo: University at Buffalo, State University of New York, 2003.
8. Moss GP, Dearden JC, Patel H. Quantitative structure-permeability relationships (QSPRs) for percutaneous absorption. Toxicology 2002;16:299-317.
9. Martin YC. Quantitative drug design. New York: Marcel Dekker; 1978.
10. Ma XL, Chen C, Yang J. Predictive model of blood-brain barrier penetration of organic compounds. Acta Pharmacol Sin 2005;26:500-12.
11. Chen C, Yang J. MI-QSAR models for prediction of corneal permeability of organic compounds. Acta Pharmacol Sin 2006;27:193-204.
12. Potts RO, Guy RH. Predicting skin permeability. Pharm Res 1992;9:663-9.
13. Flynn GL. Physiochemical determinants of skin absorption. In: Gerity TR, Henry CJ, editors. Principles of route-to-route extrapolation for risk assessment. Amsterdam: Elsevier Science Publishing Co Inc; 1990. p 93–127.
14. Lien EJ, Gao H. QSAR analysis of skin permeability of various drugs in man as compared to in vivo and in vitro studies in rodents. Pharm Res 1995;4:583-7.
15. Pugh WJ, Degim T, Hadgraft J. Epidermal permeability-penetrant structure relationships: 4, QSAR of permeant diffusion across human stratum corneum in terms of molecular weight, H-bonding and electronic charge. Int J Pharm 2000;197:203-11.
16. Degim T, Hadgraft J, Ilbasmis S, Ozkan Y. Prediction of skin penetration using artificial neural network (ANN) modeling. J Pharm Sci 2003;92:656-64.
17. Degim T. Understanding skin penetration: computer aided modelling and data interpretation. Current Computer-Aided Drug design 2005;1:11-9.
18. Abraham MH, Martins F, Mitchell RC. Algorithms for skin permeability using hydrogen bond descriptors: the problem of steroids. J Pharm Pharmacol 1997;49:858-65.
19. Potts RO, Guy RH. A predictive algorithm for skin permeability-the effects of molecular-size and hydrogen-bond activity. Pharm Res 1995;12:1628-33.
20. Johnson ME, Blankschtein D, Langer R. Evaluation of solute permeation through the stratum corneum: Lateral bilayer diffusion as the primary transport mechanism. J Pharm Sci 1997;86:1162-72.
21. Patel H, Berge WT, Cronin MTD. Quantitative structure-activity relationships (QSARs) for the prediction of skin permeation of exogenous chemicals Chemosphere 2002;48:603-13.
22. PubChem Compound Browser. Bethesda (MD): National Library of Medicine (US); Available from URL: .http://pubchem.ncbi.nlm.nih.gov
23. Sontag ED. Feedback stabilization using two-hidden-layer nets. IEEE Transactions on Neural Networks 1992;3:981-90.
24. Boger Z, Guterman H. Knowledge extraction from artificial neural network models. IEEE Systems, Man, and Cybernetics Conference; 12–15 October 1997; Orlando, FL.